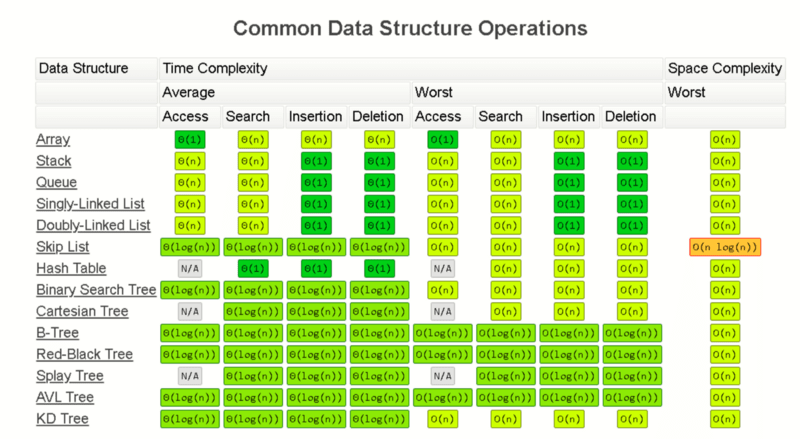
10
Quick Guide To Big O
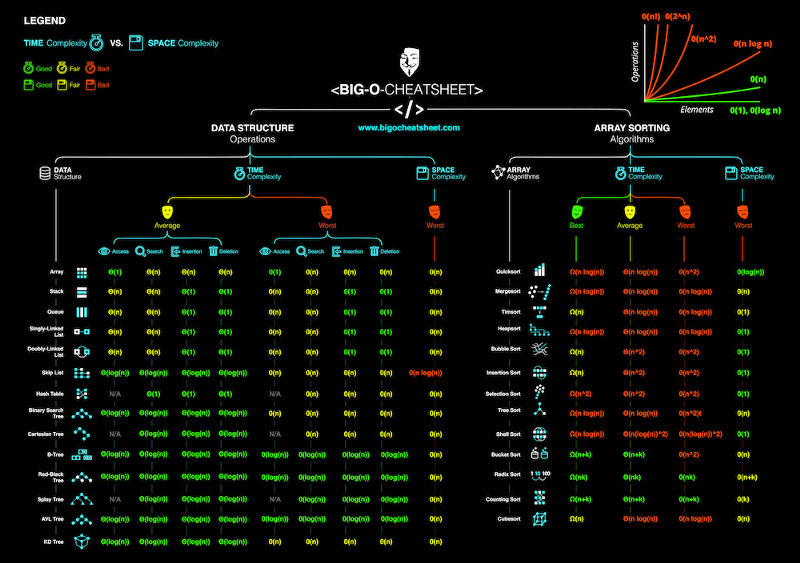
How does our performance scale?.Smaller Big O is better (lower time complexity)Simplify Products : If the function is a product of many terms, we drop the terms that don't depend on n.Simplify Sums : If the function is a sum of many terms, we drop the non-dominant terms.n : size of the inputT(f) : unsimplified math functionO(f) : simplified math function.Putting it all together

The algorithm takes roughly the same number of steps for any input size.
In most cases our hidden base of Logarithmic time is 2, log complexity algorithm’s will typically display ‘halving’ the size of the input (like binary search!)
Linear algorithm’s will access each item of the input “once”.
Combination of linear and logarithmic behavior, we will see features from both classes.
Algorithm’s that are log-linear will use both recursion AND iteration.
C is a fixed constant.
C is now the number of recursive calls made in each stack frame.
Algorithm’s with exponential time are VERY SLOW.

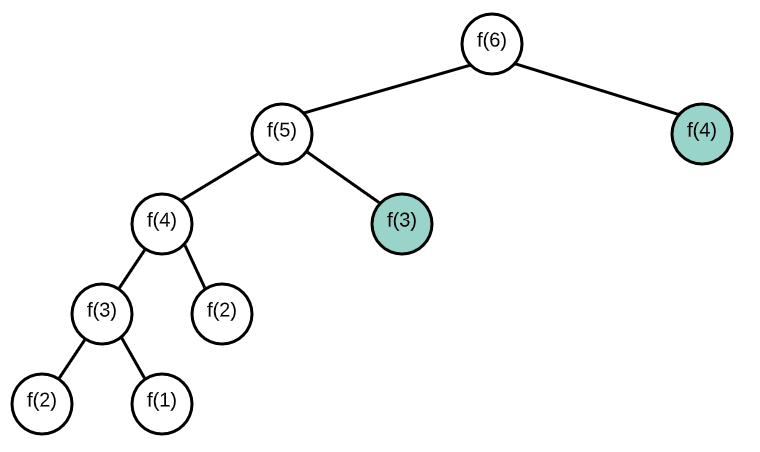
Rules:
Use When:
Normal Recursive Fibonacci
function fibonacci(n) {
if (n <= 2) return 1;
return fibonacci(n - 1) + fibonacci(n - 2);
}Memoization Fibonacci 1
Memoization Fibonacci 2
Tabulated Fibonacci
Time Complexity: Quadratic O(n^2)Space Complexity: O(1)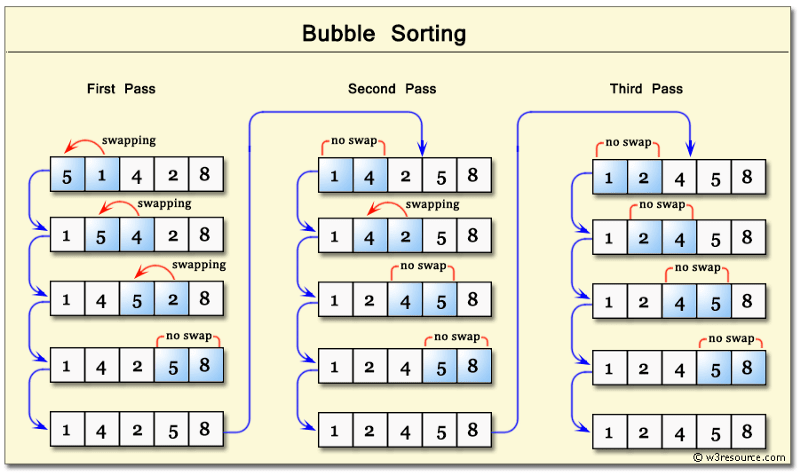
It’s almost never used in production code because:
Bubbling Up : Term that infers that an item is in motion, moving in some direction, and has some final resting destination.Time Complexity: Quadratic O(n^2)Space Complexity: O(1)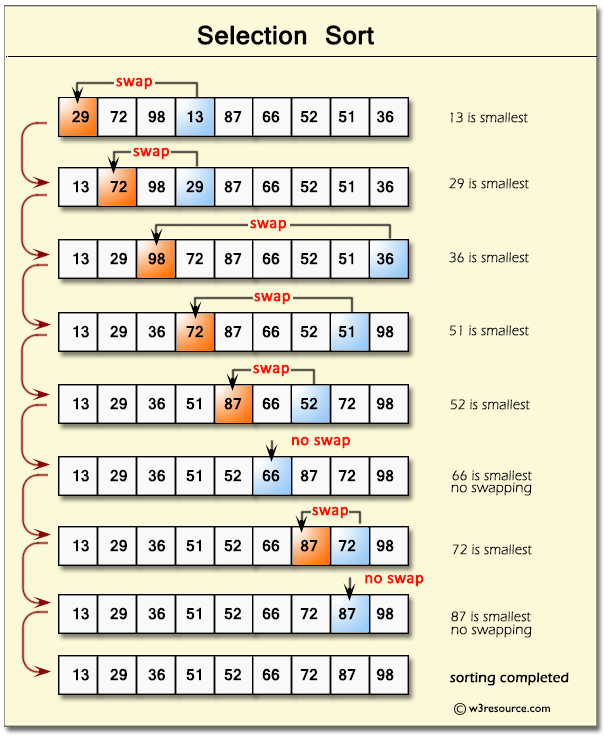
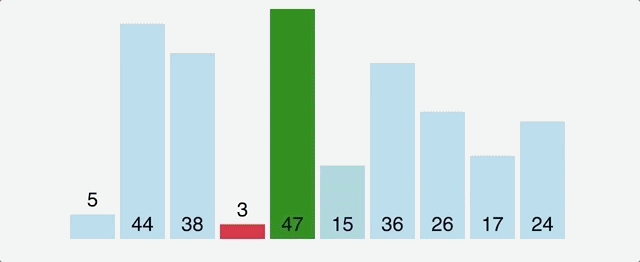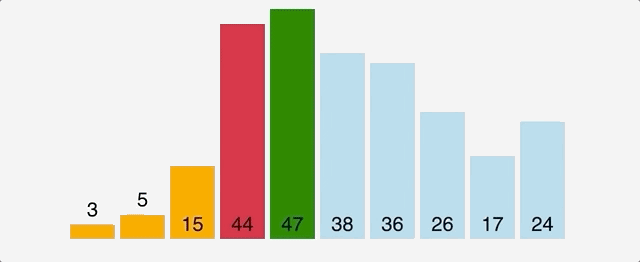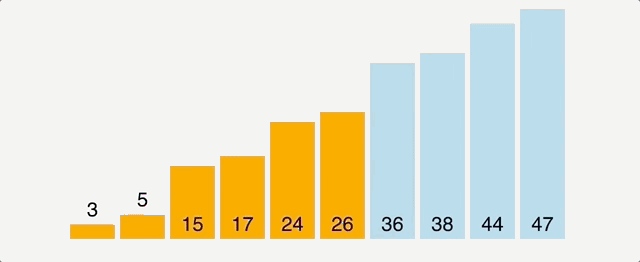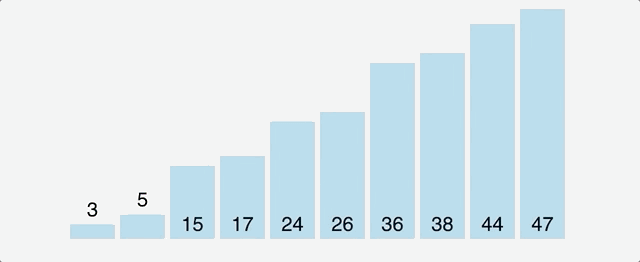
Time Complexity: Quadratic O(n^2)Space Complexity: O(n)
Time Complexity: Log Linear O(nlog(n))Space Complexity: O(n)
Steps:
Time Complexity: Quadratic O(n^2)Space Complexity: O(n)
Time Complexity: Log Time O(log(n))Space Complexity: O(1)
Min Max Solution
Steps: