17
A Brief Introduction to Dynamic Programming
Dynamic programming is a technique that can be used to solve a particular class of problems. Let's take a look at how to determine if you can use dynamic programming for a given problem, and the different approaches (top-down and bottom-up) that you can use.
To use dynamic programming, you need to be able to break down the problem into smaller subproblems. If you are sure you can do that, then you need to check if the problem has the following properties:
If a problem can be broken down into smaller subproblems and has these two properties, then you can apply dynamic programming to solve the problem and success is guaranteed!
Let's dive deeper into what each of these mean while trying to solve problem #70 - Climbing Stairs on Leetcode.
Here is what the problem statement says:
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Let us first see if we can break down the problem into smaller subproblems. Let us say that the answer we want - the number of distinct ways we can climb a staircase with
n steps, can be expressed as countDistinctPaths(n). Now, we know that we can take either one or two steps at a time. If we take one step, we need to follow the same rules to climb the remaining
n-1 steps. Similarly, if we climb two steps, we again need to follow the same rules to climb the remaining n-2 steps. So, the total number of ways we can climb the staircase is either by taking one step and then taking one of the
countDistinctPaths(n-1) paths for the remaining n-1 steps, or by taking two steps and then taking one of the countDistinctPaths(n-2) paths for the remaining n-2 steps. We can write the total number of paths we can take as follows:
countDistinctPaths(n) = countDistinctPaths(n-1) + countDistinctPaths(n-2)As you can see, we've managed to break the problem down into smaller subproblems! If we have the answer for
n-1 and n-2, then we can combine those answers to calculate the answer for n. There's one more thing we need to think about though - how small can we keep making the problems?
Well, the smallest staircase we can have is one with a single step. And there is only one way we can climb that step (since we can't take two steps in this case - because there's only a single step!) Also, if there is no staircase at all, there is no way we can climb it!
So we can rewrite the problem as:
countDistinctPaths(0) = 0 (no staircase, so no way to climb it!) countDistinctPaths(1) = 1 (only one step, only one way to climb it) For any value of n greater than 1,
countDistinctPaths(n) = countDistinctPaths(n-1) + countDistinctPaths(n-2)This kind of expression is also commonly known as a recurrence relation.
To check if there are overlapping subproblems, let us try to think about how many times we will call
countDistinctPaths if we want the answer of say a staircase with 5 steps.We know that the answer we're looking for is
countDistinctPaths(5). From our recurrence relation, we know that
countDistinctPaths(5) = countDistinctPaths(4) + countDistinctPaths(3). We can then use the recurrence relation to further break down
countDistinctPaths(4) into countDistinctPaths(4) = countDistinctPaths(3) + countDistinctPaths(2). Now if we put this back in the first expression, we get
countDistinctPaths(5) = (countDistinctPaths(3) + countDistinctPaths(2)) + countDistinctPaths(3).Similarly, we can replace
countDistinctPaths(3) with countDistinctPaths(2) + countDistinctPaths(1).The result is then
countDistinctPaths(5) = (countDistinctPaths(3) + countDistinctPaths(2)) + (countDistinctPaths(2) + countDistinctPaths(1)).If you look closely, you'll notice that we're computing
countDistinctPaths(3) and countDistinctPaths(2) multiple times. It's easier to see all the computations we have to do in the form of a tree:
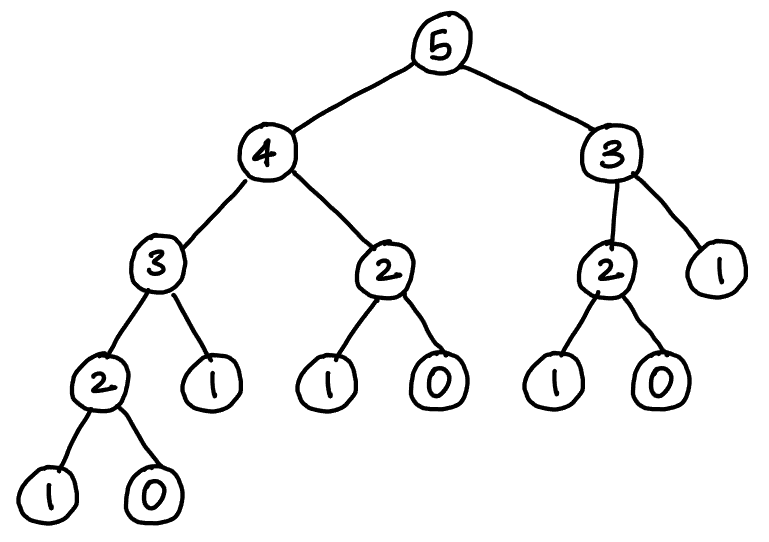
Each node in this tree is a call to
countDistinctPaths and the value in the node is the parameter we are passing to the function. As you can see, we're repeating the calls for 2 and 3. This tells us that the problem we are trying to solve has overlapping subproblems. If you can find the optimal solution to a problem using optimal solutions to its subproblems, then the problem is said to have an optimal substructure.
What this means for us is that to find the optimal solution for
countDistinctPaths(n), we need the optimal solution for countDistinctPaths(n-1) and countDistinctPaths(n-2). In this particular context, "optimal" for us means the maximum number of paths. Therefore, this problem has an optimal substructure. I personally had a tough time understanding this property and found looking at examples of problems that DON'T have optimal substructure helped understand this better. You can find a list of such problems on the optimal substructure page on Wikipedia.
Once you have verified that a problem can be solved using dynamic programming, there are two approaches you can use to solve it: the top-down approach or the bottom-up approach. Let's take a closer look at each of these.
The top-down approach involves converting the recurrence relation we wrote to recursive function calls and then making some minor tweaks to prevent the repeated evaluation of the overlapping subproblems.
Let's start with a recursive implementation of our recurrence relation in JavaScript:
function countDistinctPaths(n) {
// If there are no stairs
if (n === 0) {
return 0;
}
// If there is only one stair
if (n === 1) {
return 1;
}
// The recurrence relation
return countDistinctPaths(n-1) + countDistinctPaths(n-2);
}As we saw in the tree above, this plain recursive implementation makes repeated calculations for the overlapping subproblems. These repeated calls mean we are spending time calculating the same values over and over again. And the number of repeated calls is much higher for larger values of
n so we're wasting a lot of time!With dynamic programming, we can compute the value of each subproblem just once and store it in memory - a technique called "memoization" (nope, not a typo, it's not memorization. See this Wikipedia page for how this term was coined). The next time we encounter the same subproblem and need to calculate the value, instead of using the recurrence relation, we can just retrieve the result from memory!
// We've added "memo"ry to store values we compute. It is empty in the beginning.
function countDistinctPaths(n, memo={}) {
// If there are no stairs
if (n === 0) {
return 0;
}
// If there is only one stair
if (n === 1) {
return 1;
}
// Check if we have already computed this before
if (n in memo) {
return memo[n];
}
// The recurrence relation with two minor tweaks:
// 1. We store the computed value in memo[n] for future use
// 2. We pass the memory object to the recursive calls
return memo[n] = countDistinctPaths(n-1, memo) + countDistinctPaths(n-2, memo);
}This approach is called top-down because we start with the biggest problem first,
countDistinctPaths(n) and keep recursively breaking it down into smaller problems until we reach the smallest possible subproblems - countDistinctPaths(0) and countDistinctPaths(1). With the bottom up approach, we start from the smallest subproblems and iteratively combine them until we find a solution to the original problem.
For us, this means we start with
countDistinctPaths(0) and countDistinctPaths(1)to which we know the answer, and then combine them to get the answer to countDistinctPaths(2) and then countDistinctPaths(3) and so on until we find the answer to countDistinctPaths(n). We need a way to store the value of
countDistinctPaths(n) for each value of n. This storage is commonly known as a "table" and this bottom-up approach is also commonly called "tabulation". As you can see, there is no recursion involved here. Just good old iteration!
function countDistinctPaths(n) {
// Our "table" to store the result for each value of n
const table = new Array(n + 1);
// The case with no stairs
table[0] = 0;
// The case with one stair
table[1] = 1;
// We keep combining subproblems until we find a solution to the original problem
for (let i = 2; i <= n; i++) {
table[i] = table[i-1] + table[i-2];
}
return table[n];
}And that's it! Once the loop finishes, we'll have the result we need at index
n of the table. Like the title of this post says, this was just a brief introduction dynamic programming. The example I chose to work with was quite simple. There will be more complicated questions in which either the recurrence relation is not very obvious, or you need a two or even three dimensional table. The only way to get used to identifying if you can use dynamic programming to solve a particular problem and if so, how you can break down the problem and identify the key components is by practice.
To practice problems, I highly recommend LeetCode. Here's a list of all the dynamic programming problems on LeetCode. LeetCode has great quality questions for every topic. But my personal favorite feature on LeetCode is the Discussions tab in each problem. After you've solved the problem you can see and discuss how others are solving the same problem. Learning from other, more experienced programmers has always worked great for me.
So go ahead and start solving problems! Even better, make a challenge out of it! I'm currently doing a "100 Days of Code" challenge (which I log in this repo on GitHub) where I try to spend at least an hour every day solving problems on LeetCode or other similar sites.
17
