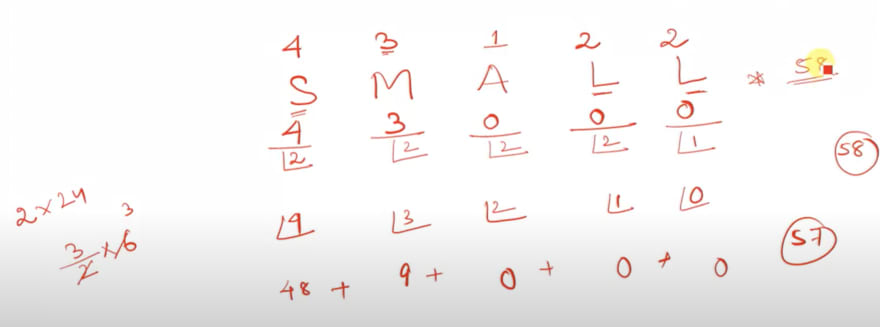HackerEarth: Rank of a word in Dictionary

This is part of a series of Leetcode and other curated solution explanations (index).
If you liked this solution or found it useful, please like this post.

HackerEarth Problem (Medium): Rank of a Word

Rank of a Word

Problem

Cham was studying Permutation and Combinations . He was deeply fascinated by the problem that asks to calculate the rank of the word S in a dictionary (given that the dictionary only comprises of the alphabets that are present in S and all the words in the dictionary have the same length as S and same number of alphabets as in S )

For the calculation procedure please refer to the given link :- Rank of a Word

Your task is simple help Cham to calculate the Rank of words .

Solution

Rank of a word is basically deduced from making all combinations of the alphabets from the given word - sorting them in order as in dictionary and checking the position of our given word.

For example word = BALL

all possible combinations = 4!/2! (as L appears twice) = 12

sort them -> [A, B, L, L]

1 : ABLL
 2 : ALBL
 3 : ALLB
 4 : BALL  -- this is our desired word
 5 : BLAL
 6 : BLLA
 7 : LABL
 8 : LALB
 9 : LBAL
10 : LBLA
11 : LLAB
12 : LLBA

so the rank is 4

Let us take few examples to understand it better.

Let's start with the words “RAIN” and “SOCCER”

The word rain has four alphabets and all of them are different. Hence, the number of words that can be formed using all the alphabets of the word “RAIN” are 4!=24.

Similarly, the word soccer has six alphabets, of which 2 are similar (C is repeated twice). Hence, the number of words that can be formed using all the alphabets of the word “SOCCER” are 6!/2! = 360.
This is the first step.

Step 1: Find the total number of words that can be formed using all the alphabets of the given word.

Once you have done that, your next step shall be to arrange the alphabets of the word in chronological order. Thus, the letters of the word rain shall be arranged as {A, I, N, R} and the letters of the word “soccer” shall be arranged as {C,C,E,O,R,S}. It shall be noted that since C appeared two times in soccer, it shall be written two times here also. This is your second step.

Step 2: Arrange all the letters of the word in alphabetical order. If few letters are repeated in the original word, repeat them the same number of times here also.

Now, here we are ready to fetch the big fish a.k.a step 3. Suppose we had to find the rank of the words “rain” and “soccer” itself.

{A,I,N,R}

Pick A. Once you have done that, you are left with three alphabets all different, from which you can form 3!=6 words. But none of these words can be rain, since rain stars with R and not A. So you can be pretty sure that the rank is nowhere from 1 to 6. (Agree?)

Next, pick I. Once you have done that, you're again left with three alphabets all different, from which 3!=6 words can be formed, none of them being rain, since rain starts with R and not I. Safe to say the rank of the word is nowhere from 7 to 12. (Agree?)

Similarly, we shall pick N next and can say that the rank of the word “rain” is nowhere from 13 to 18.

We shall now pick up R. Now we are left with {A,I,N} in the order. The 6 words that can be formed are

Rain
Rani
Rian
Rina
Rnai
Rnia

Clearly, rain is the first among these 6, making it the first after previous 18. Thus the rank of the word rain is 19.

{C,C,E,O,R,S}

Pick C. Once you have done that, you're left with 5 alphabets all different, from which you can form 5!=120 words. But none of these words can be soccer, since soccer starts with S and not C. So, you can be pretty sure that the rank is nowhere between 1 to 120. (Agree?)

There's no need to pick the second C, since you have already picked one. (This is one of the most common mistakes students do).

Next, pick E. Once you have done that, you're now left with 5 alphabets of which two are similar. Thus, the number of words that can be formed which start with E are 5!/2!=60, none of which can be soccer. Thus, no rank from 121 to 180.

Similarly, pick O and you can say no rank possible from 181 to 240. Pick R and no rank possible from 241 to 300.

Finally (the Rock has come to…), let's pick S.
Now, we have {C,C,E,O,R}. Pick C as the second letter and 4!=24 words now start with SC. No word possible from 301 to 324.
Pick E = 4!/2! = 12 -> Similarly, rank 325 to 336 is taken by SE.
Now, we SO from 337 to 348. Our soccer lies here only. Fortunately, if you arrange alphabetically now, you would find soccer has 337th rank.

Implementation

So the theory is done - lets see it in code (this handles both unique and with duplicate cases)

create a map of all characters and their occurrences

public static long findRank(String word) {
        long rank = 1;
        long suffixPermCount = 1;
        final Map<Character, Integer> charCounts = new HashMap<>();

        for (int i = word.length() - 1; i >= 0; i--) {
            char x = word.charAt(i);
            int xCount = charCounts.containsKey(x) ? charCounts.get(x) + 1 : 1;

            charCounts.put(x, xCount);

            for (Map.Entry<Character, Integer> e : charCounts.entrySet()) {
                if (e.getKey() < x) {
                    rank += suffixPermCount * e.getValue() / xCount;
                }
            }

            suffixPermCount *= word.length() - i;
            suffixPermCount /= xCount;
        }

        return rank;
    }