45
Deep Learning Library From Scratch 1: Feedforward networks
Hello! Welcome to this first post in a series where we try to build our own deep learning library in Python.
In this post, we will go begin to write a simple feedforward neural network.
We will only work on the forward pass in this post and we will work on training our network in the next post.
This post will cover how basic feedforward neural networks take in a input and produce an output from it.
Neural networks are a machine learning technique which is loosely inspired by the model of the brain.
As with all machine learning techniques, it learns from a dataset which contains inputs and their corresponding outputs.
Neural networks consist of layers. Each layer is connected to the next layer with weights and biases. These weights and biases are used by the network to calculate the output it will give. They are adjusted when the network trains, so that the network produces the optimal output based on the data it trained on.

This diagram shows a 3 layer neural network. The lines connecting the nodes are used to represent the weights and biases of the network
Each layer has its own weights and bias.
The weights and biases initially start as a matrix of random values.
A basic feedforward neural network consists of only linear layers.
Linear layers produce their output with the following formula
x @ w + b
Where...
x is the input to the layer
w is the weights of the layer
b is the bias of the layer
(@ means matrix multiply)The output of each layer is fed as an input into the next layer.
If you are unaware of how matrix multiplication works, this website here explains it nicely.
This is all we will cover for now - next post we will get into the mathematics behind how these weights and biases get corrected in training!
Layers of neural nets are composed of nodes.
Activation functions are applied to layers to determine which nodes should "fire"/"activate". This "firing" is observed in the human brain too, hence why it was introduced in neural networks, since they are loosely based of the model of the brain.
Activation functions also allows the network to model non-linear data. Without activation functions, the neural network would just be a linear regression model, meaning it would not be able to model most real world data.
There are multiple activation functions, but here are the most common ones used...
The sigmoid function maps inputs to a value between 0 and 1, as shown in the graph below.

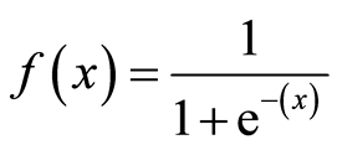
(x is the input vector)
The Relu function only allows positive values of the input vector to pass through. Negative values are mapped to 0.
For example,
[[-5, 10]
[15, -10] --> relu --> [[0, 10]
[15, 0]]

Tanh is similar to Sigmoid, except it maps inputs to values between -1 and 1.

Softmax takes in an input and maps it out as a probability distribution (meaning all the values in the output sum to 1).

(z is the input vector, K is the length of the input vector)
We will need numpy for our matrix operations...
import numpy as npFirst, let's write our linear layer class
class Linear:
def __init__(self, units):
#units specify how many nodes are in the layer
self.units = units
self.initialized = False
def __call__(self, x):
#initialize weights and biases if layer hasn't been called before
if not self.initialized:
self.w = np.random.randn(self.input.shape[-1], self.units)
self.b = np.random.randn(self.units)
self.initialized = True
return self.input @ self.w + self.bExample usage...
x = np.array([[0, 1]])
layer = Linear(5)
print (layer(x))
# => [[-2.63399933 -1.18289984 0.32129587 0.2903246 -0.2602642 ]]Now let's write all our activation function classes, following the formulae given previously
class Sigmoid:
def __call__(self, x):
return 1 / (1 + np.exp(-x))
class Relu:
def __call__(self, x):
return np.maximum(0, x)
class Softmax:
def __call__(self, x):
return np.exp(x) / np.sum(np.exp(x))
class Tanh:
def __call__(self, x):
return np.tanh(x)Now let's write a "Model" class, which will act as a container for all our layers / the actual neural network class.
class Model:
def __init__(self, layers):
self.layers = layers
def __call__(self, x):
output = x
for layer in self.layers:
output = layer(x)
return outputSave all of those classes into "layer.py" (or any name you wish).
Now we can build a simple neural network, with our tiny library so far
import layers
import numpy as np
#inputs array
x = np.array([[0, 1], [0, 0], [1, 1], [0, 1]])
#network uses all the layers we have designed so far
net = layers.Model([
layers.Linear(32),
layers.Sigmoid(),
layers.Linear(16),
layers.Softmax(),
layers.Linear(8),
layers.Tanh(),
layers.Linear(4),
layers.Relu(),
])
print (net(x))Output:
[[0. 3.87770361 0.17602662 0. ]
[0. 3.85640582 0.22373699 0. ]
[0. 3.77290517 0.2469388 0. ]
[0. 3.87770361 0.17602662 0. ]]45
