Regular Star Polygon with Python Turtle

If you are a doodler, you most certainly have doodled a pentagram or the Star of David at some point in your life.

Pentagram	Star of David

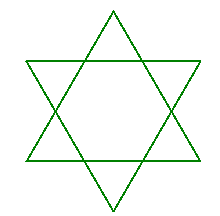Maybe some of you have also tried to add more lines to draw even more complex stars. Did you know that these stars had names too?

Heptagram	Octagram

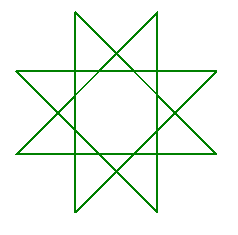Anyways, I thought that it might be fun to try drawing these stars with Python. So let's begin drawing these polygons

A star is a polygon?

Turns out that the stars above are a class of polygons called complex polygons. Basically, as opposed to normal polygons, the lines intersect each other in complex polygons

A complex polygon	A complex polygon of star shape

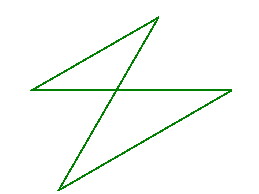The star polygon is a type of complex polygon. And there are two types. You must have realized that to draw the Star of David on a piece of paper, you have to lift your pen, but you don't have to do so to draw a pentagram. The former type of stars are called regular star polygons whereas the latter type are called degenerate star polygons

Regular octagram	Degenerate octagram

Rules of regular star polygons

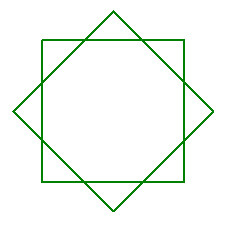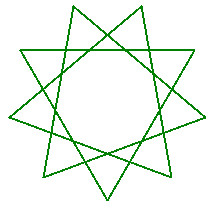
As you may have noticed above, we can draw a star with a certain number of vertices in multiple ways. For example you can draw a star polygon with 9 vertices as follow:

Method 1	Method 2	Method 3

1 vertex skipped	2 vertices skiped	3 vertices skipped

To understand what's going on count the number of vertices skipped in each of the above diagrams. Also notice that when 2 vertices are skipped the star is degenerate whereas in the other cases the star is regular. You can try to skip more vertices but you will end up drawing the same stars.

Here are the rules and formulas which are going to be useful for us

For a star with N vertices you can draw abs(N/2)-1 stars

For example for a star with 9 vertices you can only draw abs(9/2)-1=3 stars

The order of a star M can be defined as the number of vertices skipped +1.

So the possible orders for a 9-vertex star are 2, 3 and 4 for 1, 2 and 3 vertices skipped respectively

If N is divisible by M, the star is degenerate

Exterior angle of a star

Before we trace the star we need to know the angles, specifically the exterior angles. This is to know how much to turn the turtle after each forward move. We will not be rigorously deriving a formula but will simply try to understand the following:

When the turtle starts at a point, goes around then returns, 360 degrees are turned in one full rotation always (also the reason why sum of exterior angles of a polygon = 360 degrees)

In case of a star, the turtle performs multiple full rotations

The number of rotations is equal to the order of the star - M

Therefore, the sum of exterior angles of a star is 360*M

Which means that for a regular star with N vertices each exterior angle = 360*M/N

Hope that's convincing enough

Enough talk let's draw

Now that we understand our favorite doodle, we are ready to code it in Python turtle. Notice that the angle of turn is set to what we just discussed

import turtle as t

LENGTH=500

def regular_star(n,m):
    """Draws a regular star polygon (not a degenerate one)
       n = number of pointies
       m = number of points to skip
    """

    angle = 360*m/n 

    for count in range(n):
       t.forward(LENGTH)
       t.right(angle)


t.hideturtle()
t.pensize(2)
t.color("green")

regular_star(103,51)

The above code only draws any regular star polygons (the one which can be drawn without lifting the pen). We will leave it to another post to draw a degenerate star

Here's a 103 pointed star