All Star Polygons with Python Turtle

In the previous article we showed how to draw a regular star polygon which was not degenerate i.e it could be drawn without lifting the pen from the paper. In this one we will attempt to come up with a way to draw two types star polygons.

By two types I mean degenerate (must lift pen) and non-degenerate/regular (no lift pen) but I don't know the true names of these star polygons types. But I hope I get the idea across

Repeated regular polygon method

In this method we are going to look at how to draw a degenerate star polygon by repeatedly drawing regular polygon polygons (like triangles, squares and pentagons)

The Star of David

Let's begin with the simplest degenerate star we know of the Star of David. This type of star can be draw by simply drawing one equilateral triangle and then overlapping it with another one which is upside down

Note that you can draw a triangle using the circle function! See the code below

import turtle as t

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

LENGTH=200

t.circle(LENGTH)
t.circle(LENGTH,steps=3)
t.circle(LENGTH,steps=4)
t.circle(LENGTH,steps=5)

In the code above, we are drawing a triangle, square and a pentagon inscribed within the same circle making use of the steps parameter. Here's what we get:

Now we know how to use the steps argument, we can use it twice from two different places on a circle to draw our star

import turtle as t

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

LENGTH=200

def star_of_david():
    """Draws two overlapping triangles
    """
    t.circle(LENGTH,steps=3)
    t.penup()
    t.circle(LENGTH, 180)
    t.pendown()
    t.circle(LENGTH,steps=3)

t.circle(LENGTH)
star_of_david()

In the code above t.circle(LENGTH, 180) makes the turtle go to the top of the circle so that it can draw another triangle from there. Here's what we get

Degenerate Octagram

You can draw a degenerate octagram using a similar method

import turtle as t

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

LENGTH=200

def degenerate_octagram():
    t.circle(LENGTH,steps=4)
    segments=8
    t.circle(LENGTH,360/segments)
    t.circle(LENGTH,steps=4)

t.circle(LENGTH)
degenerate_octagram()

After drawing the first square, we are moving the turtle to a location determined by 360 / segments. segments = 8 because an octagram has 8 equal segments.

Remember that a n-gram star has n equal segments

Degenerate enneagram

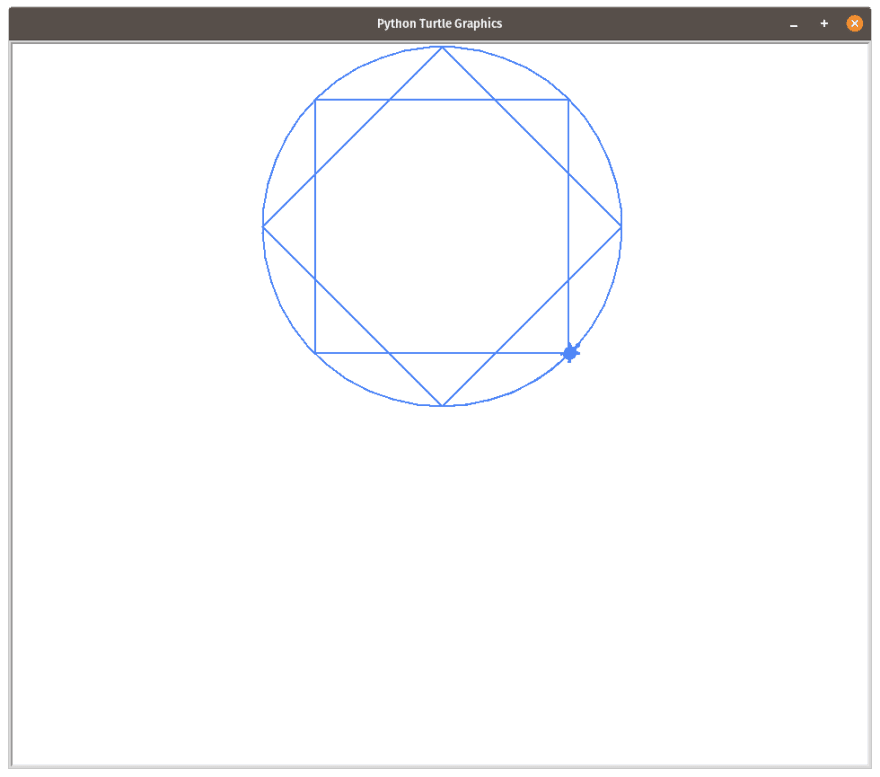
According to wikipedia, enneagram is a 9 pointed star. Unlike the hexagram and the decagram, the enneagram cannot be drawn with just two regular polygons. But how many do we need?

A degenerate enneagram should be drawn by using 3 equilateral triangles (You can try drawing this on a piece of paper too).

import turtle as t

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

LENGTH=200

def enneagram():
    segments=9

    t.circle(LENGTH, steps=3)
    t.circle(LENGTH, 360/segments)
    t.circle(LENGTH, steps=3)
    t.circle(LENGTH, 360/segments)
    t.circle(LENGTH, steps=3)

t.circle(LENGTH)
enneagram()

In the code above, we are calling the circle(LENGTH, steps=3 function 3 times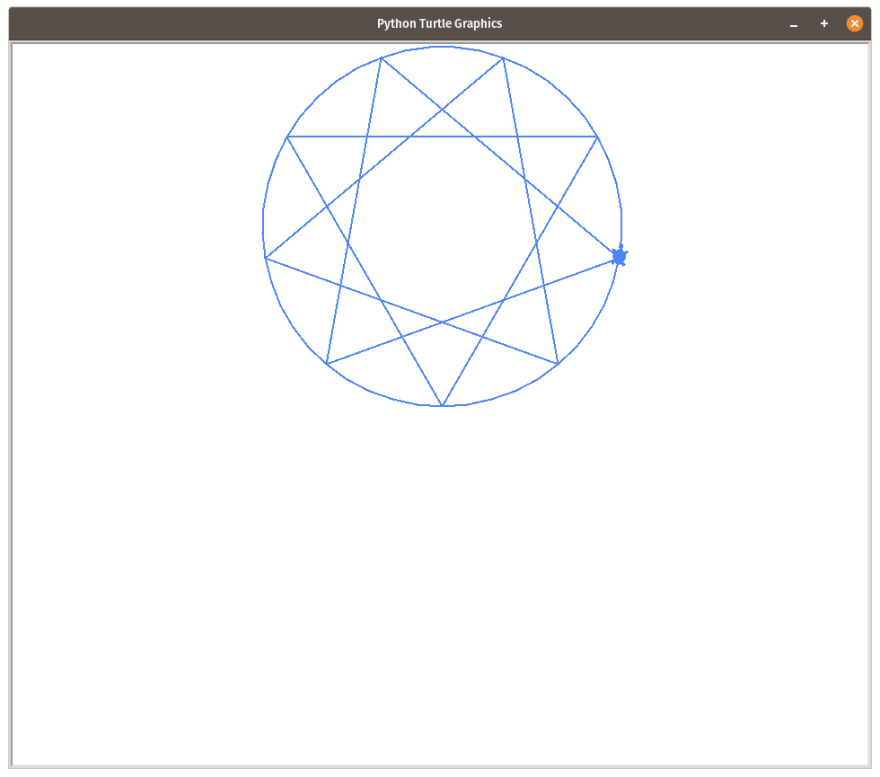

A General method - 1 (Regular non star Polygon based)

Now, how do we know the number of times we need to repeat the circle and step commands? To answer that we can make a few observations about the examples above:

A hexagram is a (6,2) star where the vertices - 6 is divisible the order- 2, 3 times

A octagram is a (8,2) star where the vertices - 8 is divisible the order- 2, 4 times

A enneagram is a (9,3) star where the vertices - 9 is divisible the order- 3, 3 times

With the above, we might be able to say that for a degenerate n-gram with the order m, the quotient of n/m is the number of sides of the polygon while the order m is the number of times we need to draw the polygon

So, we should try the following:

For an n,m degenerate star draw m number of regular polygons
And the polygons drawn should have n/m sides

Let's code that

import turtle as t

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

LENGTH=200

def degenerate(n,m):
    segments = n
    order = m

    sides = int(n/m)

    for _ in range(order):
        t.circle(LENGTH, steps=sides)
        t.circle(LENGTH, 360/segments)

t.circle(LENGTH)
degenerate(10,2)

The code above works! It drew the 10 gram and the 12 grams below

(10,2)	(12,2)

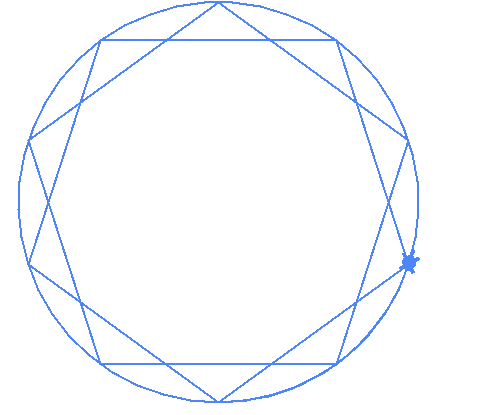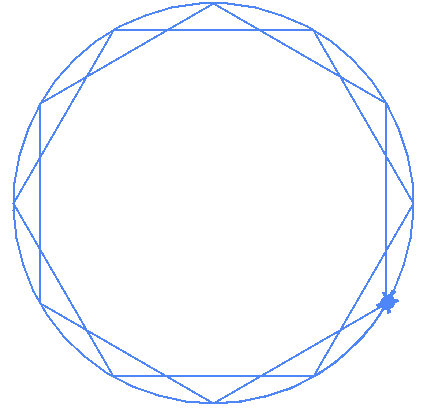You can also draw (12,3) and (12,4)

(12,3)	(12,4)

Interestingly if you try to draw (10,5) and (12,6) it draws this:

(10,5)	(12,6)

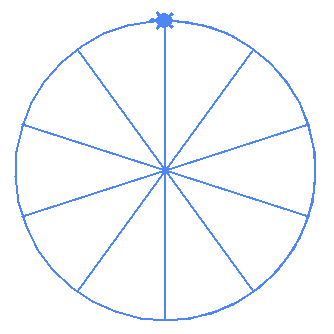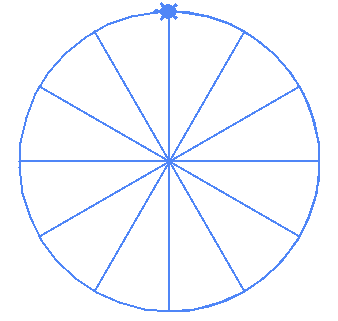This is a reminder that the possible orders (values of m) are
2 through (n-1)/2-1. Basically the order can't be 1 and it also can't be half of the number of vertices

With the general code above, have we covered all the degenerate regular star polygons?

The (10,4) star

In the examples that we have looked at a degenerate star polygon can be composed of multiple regular (non-star) polygons. But (10,4) is a curious case. In the previous article we had written a code that draws regular stars. Let's see what happens when we use it here

import turtle as t

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

LENGTH=150

def regular_star(n,m):
    """ n = number of pointies
        m = order of the star,
            (number of skips + 1)
    """

    angle = 360*m/n

    for count in range(n):
       t.forward(LENGTH)
       t.right(angle)

regular_star(10,4)

Yes we get a pentagram! But we were supposed to have 10 vertices :(

A new type of degenerate

Hence, (10,4) is a new type of degenerate star where n is not divisible by m and as such we cannot draw it with the degenerate function we wrote earlier.

We can draw this type of degenerate stars by overlapping two stars. Unfortunately we cannot use the circle's step parameter anymore. We need to draw a regular star then rotate it to draw another star. To do that we will first begin by modifying our regular_star function as follows

def regular_star(n,m):
    """ n = number of pointies
        m = order of the star,
            (number of skips + 1)
    """

    angle = 360*m/n

    t.left(180-angle/2)

    for count in range(n):
       t.forward(LENGTH)
       t.right(angle)

    t.right(180-angle/2)

The code above adds t.left(180-angle/2) to place the regular star to the left side of the turtle. This is similar to how a circle command behaves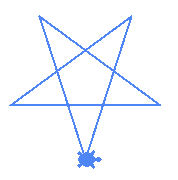

Notice above that both the stars are drawn to the left side of the turtle

We will additionally make the following changes to our code

import turtle as t
import math

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

RADIUS=150


def regular_star(n,m):
    """ n = number of pointies
        m = order of the star,
            (number of skips + 1)
    """

    angle = 360*m/n
    center_angle = 2*m*math.pi/n

    t.left(180-angle/2)


    length=2*RADIUS*math.sin(center_angle/2)

    for count in range(n):
       t.forward(length)
       t.right(angle)

    t.right(180-angle/2)

regular_star(7,2)
t.circle(RADIUS)

In the code above, we have made the following changes

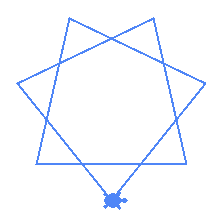
Replaced the global LENGTH with RADIUS. This is to allow us to draw the star of a defined radius

Computed a center angle which is the angle subtended by m segments on the center of the circle. center_angle is the representation of arch length in radians

We used the center_angle and the RADIUS to compute the length of the arms of the star

(5,2)	(7,2)	(7,3)

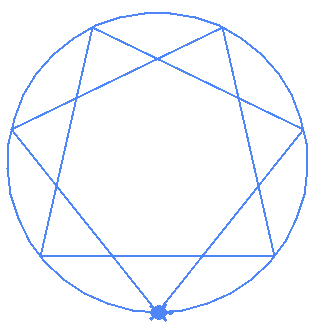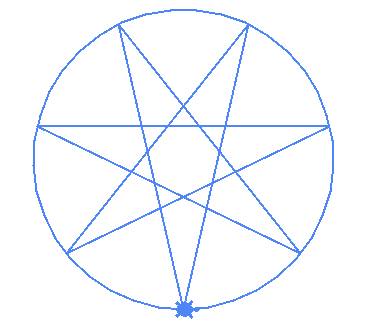We can now draw a star to the left side of the turtle having defined radius. We can even overlap them all

A better general method

Our goal is to build a better general method to draw any degenerate regular polygon star of a given number of vertices and order. Let's begin again by listing the properties of the degenerate stars

Star	Properties
(6,2)	2 overlapping triangles
(8,2)	2 overlapping squares
(9,3)	3 overlapping triangles
(10,4)	2 overlapping pentagrams
(14,4)	2 (7,2) stars
(14,6)	2 (7,3) stars
(15,6)	3 overlapping pentagrams

The above can be verified by trying them out on a piece of paper (or by just thinking way too hard)

Here's an algorithm that we might be able to use to draw all the of the above stars

Find the greatest common divisor (gcd) of n and m

Divide n and m by the gcd to obtain a star (n/gcd,m/gcd)

Draw the (n/gcd,m/gcd) star

Move the turtle to another position on the circumcircle determined by 360/n degrees

Repeat 3 until we have drawn the star gcd number of times

Let's try it:

import turtle as t
import math

t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)

RADIUS=150

def regular_star(n,m):
    """ n = number of pointies
        m = order of the star,
            (number of skips + 1)
    """
    angle = 360*m/n
    center_angle = 2*m*math.pi/n

    t.left(180-angle/2)

    length=2*RADIUS*math.sin(center_angle/2)

    for count in range(n):
       t.forward(length)
       t.right(angle)

    t.right(180-angle/2)


def star(n,m):
    """ n = number of pointies
        m = order of the star,
            (number of skips + 1)
    """
    gcd = math.gcd(n,m)
    new_n = int(n/gcd)
    new_m = int(m/gcd)
    segment_angle = 360/n

    for _ in range(gcd):
        regular_star(new_n, new_m)
        t.penup()
        t.circle(RADIUS, segment_angle)
        t.pendown()

star(10,4)

With the code above it turns out that when the gcd is 1, we get either a regular non-degenerate star or a polygon. So we have written code to generalize:

Regular Polygons

Regular Non-degenerate stars!

Regular degenerate stars!~

Weird stick star :)

Examples:

Name	Drawing
(10,1)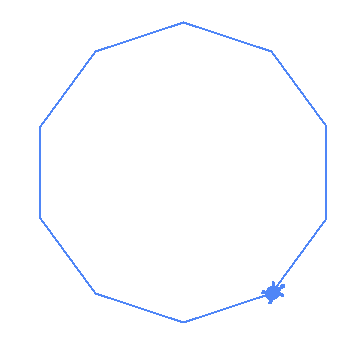
(10,2)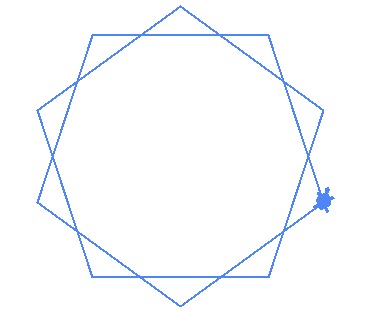
(10,3)
(10,4)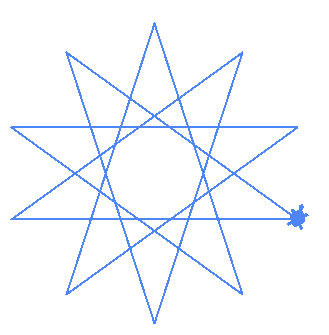
(10,5)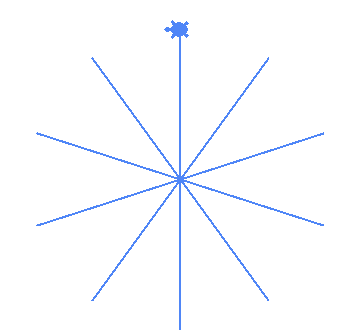
(14,4)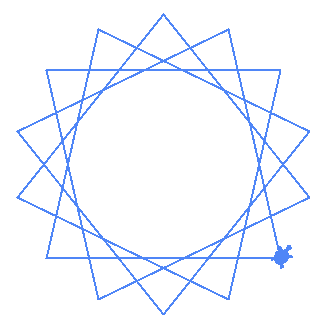
(14,6)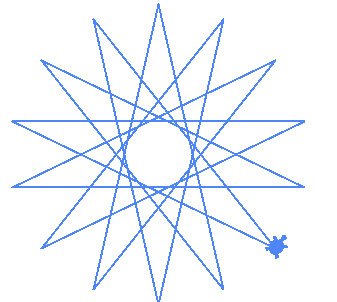
(15,6)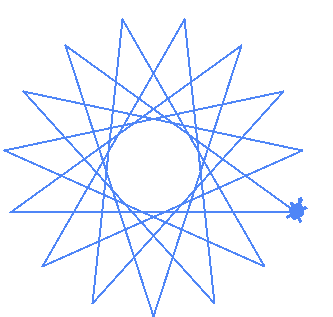

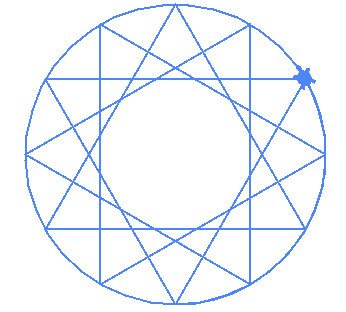
Bonus

You can overlap all orders for a fixed number of vertices to get beautiful images such as these

def all_stars(n):
    for x in range(int(n/2)):
        star(n,x+1)


all_stars(10)
t.hide()

Yay!!~

Categories:

Python

Tags:

Python Turtle Geometry Math

NodeJS vs Python

App Development Practices To Follow For Your Business In 2021

Generating Combinations using C++

Creating a Podcast of book summaries and articles in PDF in Portuguese with AI in Python!

Getting started with Docker & Flask.

21 must-read books for kids, beginner, advanced & interview with PDF 🐍

Weekly Challenge 140

Logistic Regression

All Star Polygons with Python Turtle

Categories:

Tags:

Related Posts